[Math] Matrice, avancée partie 1

• Transposition 

La transposée A^T (aussi notée A') d'une matrice A est la matrice obtenue en échangeant les lignes et les colonnes de A :

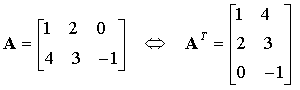
La transposée d'un vecteur-colonne est un vecteur-ligne :

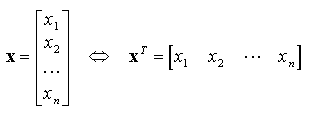
• Inversion d'une matrice carrée

Une matrice carrée A est dite inversible ou régulière s'il existe une matrice carrée A^-1 (appelée matrice inverse) telle que :

A × A^-1 = A^-1 × A = I

Si A^-1 n'existe pas, la matrice A est dite singulière

• Déterminant d'une matrice carrée

Pour une matrice 2 × 2, on montre que la matrice inverse est donnée par :

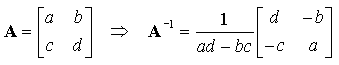
Le nombre (ad - bc) est appelé déterminant de la matrice A, noté :

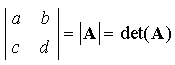
La matrice inverse A^-1 n'existe donc que si det A est différent de zéro.

La matrice A est singulière si det A = 0, régulière dans le cas contraire. Ce résultat se généralise à une matrice de dimension quelconque.

Propriétés des déterminants :

• det(A^T) = det(A)

• det(AB) = det(A) × det(B)

• Le déterminant d'une matrice triangulaire ou diagonale est égal au produit des éléments diagonaux. En particulier, det(I) = 1 (si I est la matrice unité)

• Si A est régulière, det(A^-1) = 1 / det(A)
  puisque det(AA^-1) = det(A) × det(A^-1) = det(I) = 1

• Si A est orthogonale, det(A) = ±1
  puisque det(AA^T) = [det(A)]² = det(I) = 1

• 
  

[Math] Matrice, les fondamentaux

• Introduction 

Une matrice 'x, m' est un tableau de nombres ayant 'n' lignes et 'm' colonnes. Ce sont les dimensions de la matrice.

Exemple d'une matrice avec n = 2 et m = 3

Par convention, la matrice est notée 'A' et les éléments qui la composent 'A_ij'. Où 'i' et 'j' représentent les éléments situés à l'intersection.

Une matrice dont la dimension 'm' égale à '1' est appelée vecteur colonne.

• Matrices particulières 

Matrice unité, notée I_n

Matrice diagonale, notée D_ii

Matrice triangle haut

Matrice triangle bas

• Opération mathématiques
• Addition et soustraction

• Multiplication par une constante

• Transposition d'une matrice

• Transposition d'un vecteur

• Opérations étendues
• Multiplication des vecteurs

Cette opération est appelée 'produit scalaire'. Afin de pouvoir réaliser cette opération, les vecteurs doivent avoir la même dimension.

• Multiplication des matrices

Le produit de la matrice A (n, m) par la matrice B (m, p) est la matrice C (n, p) telle que l'élément C_ij est égal au produit scalaire de la ligne i de la matrice A par la colonne j de la matrice B.